– Hoy le he traído un mapa para que me explique algo que me gustaría saber…
-¿A ver? ¡Hombre, el mapa 1:25.000 de San Muñoz! ¿Cómo es que lo tiene? ¿Algún motivo especial?
– Sí. Es que mi padre es de ese pueblo y muy aficionado a los mapas. Yo aprendí de él a leerlos y a amarlos.
– ¡Ya! ¿Y qué opina de los tiempos de ahora, en que todo el mundo maneja las imágenes que nos brindan Internet y los GPS?
– Creo que la moderna tecnología ha acercado el conocimiento a todos, pero no puede sustituir a lo que nos brinda un buen mapa, donde, además de los lugares, con su nombre, podemos ver el relieve y sacar consecuencias de todo tipo…
– ¡Exactamente! ¡Veo que piensa como yo! Es lo mismo que la diferencia entre leer un libro en papel o en una «tablet«. Pero no, un mapa nos brinda muchos más detalles que su imagen informática. Ésta puede ser una ayuda rápida, pero los detalles los apreciamos mucho mejor en el papel… ¡Claro está que hay que saber leer en ellos!
– ¡Se nota que usted también ama los mapas!
– ¡Por supuesto! Siempre que iba a un lugar nuevo me sentía como desnudo si no llevaba un 1:50.000 conmigo. O mejor el 1:25.000. Y para programar un viaje, aparte de los mapas de carreteras, el 1:200.000 era mi mejor guía… Pero, dígame: ¿qué quiere que le explique de este mapa de San Muñoz?
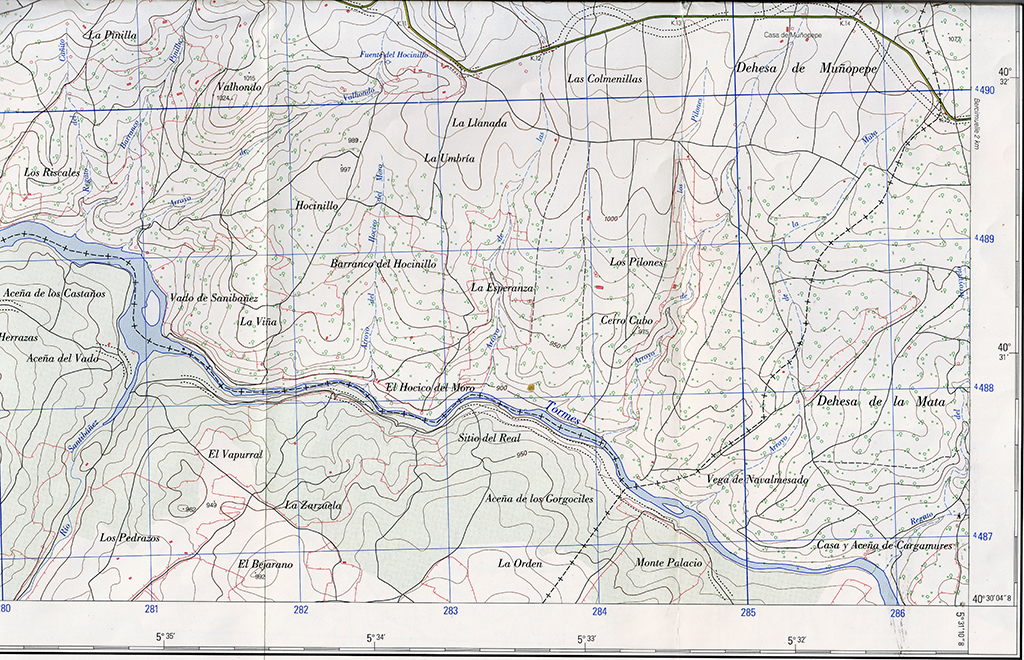
– Es esta cuadrícula azul. Supongo que es un sistema de ubicación que sustituye a la longitud y a la latitud. ¿No es así?
– ¡Efectivamente! No cabe duda de que el sistema geográfico sexagesimal tiene sus inconvenientes y por eso se le superpone el UTM.
– ¿Y en qué consiste? ¿Qué significa UTM?
– Significa Universal Transversal Mercator.
– ¿Mercator? Pero esa proyección ¿no da muchos errores? ¿No se inventó en el siglo XVI, sobre un cilindro tangente a la esfera terráquea en el ecuador?
– Pues sí. Pero eso es así a nivel global. No hay errores en la línea ecuatorial, pero conforme nos vamos alejando de ella son cada vez mayores.
– ¿Y entonces?
– Lo que se hace es poner el punto de vista no sobre el ecuador, sino encima del área a cartografiar. De todos modos recuerde que la representación de una esfera en un plano es imposible de hacer sin errores lineales, angulares o superficiales al mismo tiempo. Se puede lograr una cartografía sin errores en uno de los tres conceptos, pero los tendrá inevitablemente en los otros dos.
– ¿Y los mapas actuales a escalas 1:50.000 o 1:25.000?
– Pues, hoy por hoy, es lo mejor que se ha inventado.
-¿Y en qué consiste el sistema de coordenadas UTM?
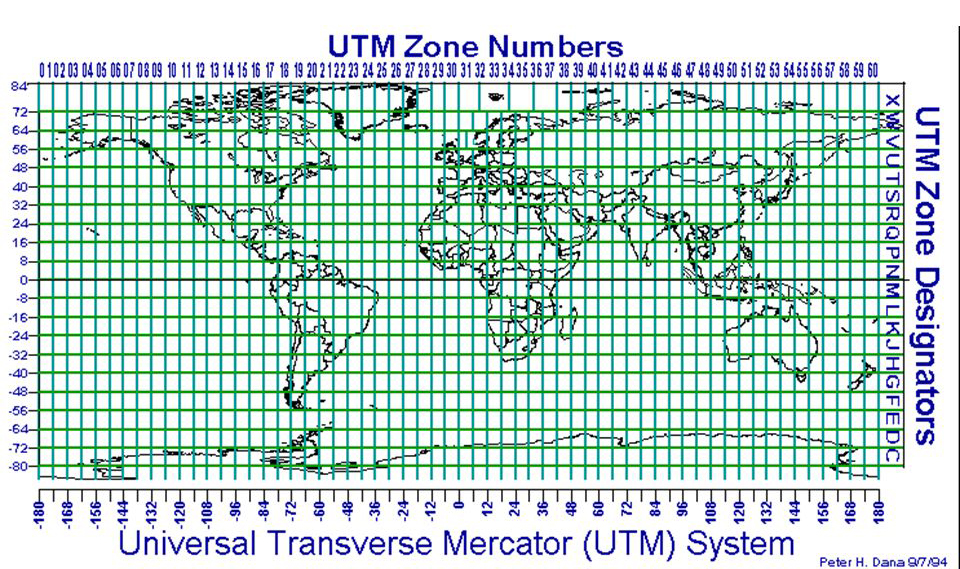
– Pues mire usted. Se divide el mapa universal Mercator en 60 zonas, que al desarrollarse formarán husos de 6º, tomando como origen la parte opuesta del meridiano de Greenwich. Éste marcará por tanto la frontera entre los husos 30 y 31. Se descartan las regiones polares, en las que se usan proyecciones estereográficas. La Península Ibérica se encuentra en los husos 29, 30 y 31, y las Islas Canarias en el 28. ¿Hasta aquí va todo bien?
-Sí, sí. Continúe…
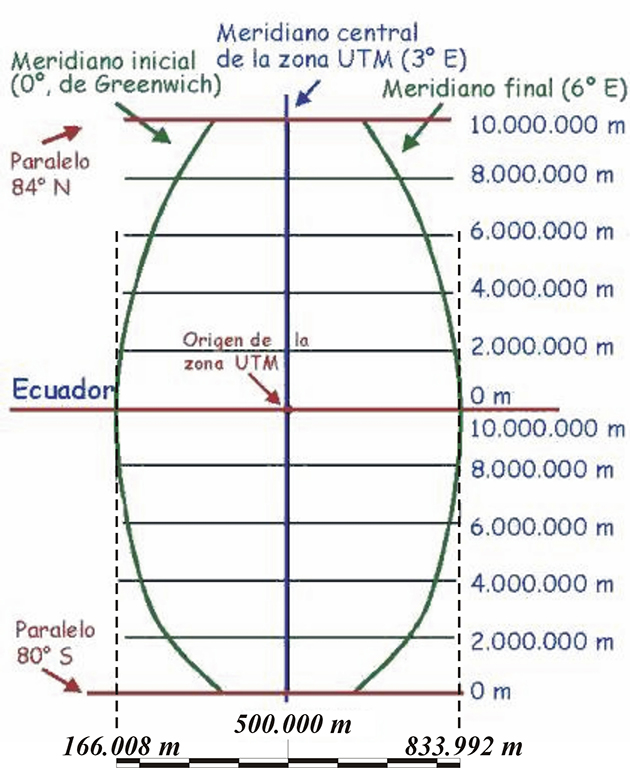
– Cada huso se divide en cuadrados de 100 km/lado (km/l), que llamaremos hectokilométricos. En cada uno de ellos el origen de coordenadas no es el borde izquierdo en el ecuador, como se hacía antes, sino el centro de cada huso, es decir el cruce del ecuador con el meridiano central. Así, en el huso 31 el meridiano central es el 3ºE. Para evitar números negativos, en dicho origen de cada huso el valor de la «x» es de 500 km. Es decir, el ecuador está entre los 166.008 y 833.992 km.
«Para el hemisferio Norte las coordenadas «y» suben progresivamente desde 0 km, pero para el hemisferio Sur, para evitar cifras negativas, se desciende desde 10.000 km.
– ¿Y la orientación al norte?
– ¡Ahí está el problema! No se puede hacer con la cuadrícula UTM. Para ello sólo son válidos los meridianos y los paralelos geográficos, que deben estar señalados en todos los mapas.
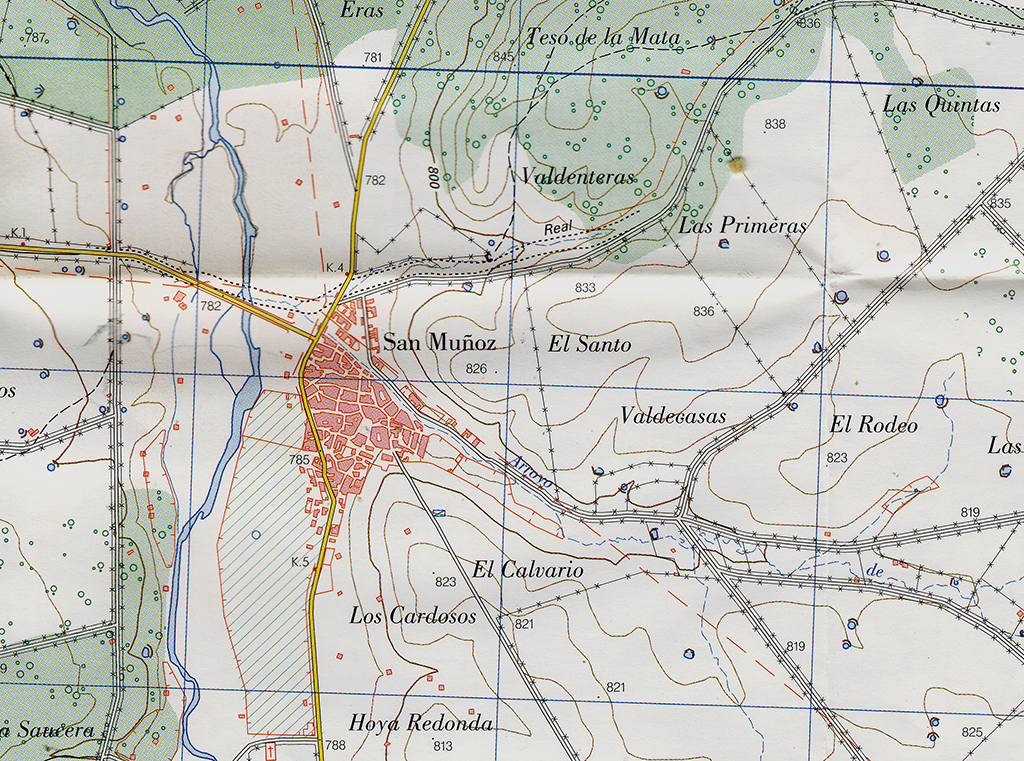
«Sigamos. Cada cuadrado hectokilométrico se define por las coordenadas de su esquina inferior izquierda, que vienen dadas en cifras: la primera es la de las «x» y las otras dos, de las «y». Por tanto, su pueblo, San Muñoz, está en el cuadrado hectokilométrico… –veamos…– 7 45, del huso 29. Pero si queremos precisar más, podemos dividir dicho cuadrado en 10×10 cuadraditos de 10 km/l. Entonces San Muñoz está en el 74 451. ¿Queremos mayor precisión? Entonces dividimos el hectokilométrico en 100×100 (o lo que es lo mismo el de 10km/l en 10×10) y tenemos que su pueblo está entre el 742 4518 y el 742 4519, que son cuadrados de 1 km/l, o kilométricos. En resumen, los cuadrados kilométricos de este pueblo están a 742-500=242 km al E del meridiano central de la zona 29 (9ºO) y a 4.518 y 4.519 km del ecuador.
«¿Queremos más? ¡Pues dividimos más! Veamos. ¡Vaya, la iglesia no se ve en el mapa! Este cruce de carreteras amarillas está en el cuadrado de 100 m/l 7422 45185. Y así podemos seguir precisando más y más dividiendo cuadrados y añadiendo dígitos antes del mediano y al final. Los cuadrados hectométricos tendrán 9 dígitos; los decamétricos, 11; los métricos 13; etc… No hay límites para este sistema de proyección UTM, pero –recuerde– no se marcan puntos sino superficies cuadradas. ¿Ha quedado claro?
– ¡Clarísimo! Y ahora, me voy a casa a practicar un poco con mis mapas.
-¡De acuerdo! Pero tenga en cuenta que si no son muy modernos, se puede encontrar con otra nomenclatura para los cuadrados de 100 km/l. Si tiene dudas, no dude en volver a consultarme.
—————-
Al llegar a mi casa me acordé de que hace unos días Lira me preguntó que dónde estaba esa angostura del río Tormes de la que le había hablado, en donde su anchura es de escasos metros.
Con lo explicado ahora, y a la vista de los mapas 1:25.000 números 528-IV Guijuelo) y 553-II (Santibáñez de Béjar) le contesto:
- Hay que precisar que el lugar se encuentra en el huso 30. Tomamos un camino que parte cerca de Santibáñez de Béjar en 2788 44854. (Al dar 9 dígitos quiere decir que estoy hablando de cuadrados hectométricos)
- Podemos dejar el coche al pie de un puente sobre el arroyo Santibáñez, en 2797 44858. Desde allí iremos andando.
- Llegamos a un ensanchamiento del río Tormes, en 2809 44882.
- Encontramos la angostura del Tormes en 2818 44878.
¡Feliz excursión, Lira!